【印刷可能】 階差数列の和 等比数列 876854

数学B（数列）：「等差数列」×「等比数列」型 オンライン無料塾「ターンナップ」 対象 高校生 再生時間 1145 説明文・要約 ・一般項：a n ＝「等差数列の一般項」×「等比数列の一般項」 ・和（S n ＝a 1 ＋a 2 ＋＋a n1 ＋a n ） → 等比等比数列の和(Sn)を等比級数といい、次式の公式となる。 Sn = a ar ・・・ ar n1 = a(1r n1)/(1r) r ≠1 Sn = na r=11階差数列 数列 の階差数列が扱いやすい数列の場合。 (19) の各項は、 ～ の和をとることで以下のように得られる。 () 例 の階差数列が で のときの数列 は以下のようになる この数列の一般項は、 (21) 上式は の時も初期条件 を満足する。

3

階差数列の和 等比数列

階差数列の和 等比数列- A, B, Cは等比数列の連続する3項であるので、 A = 1/r×B C = r×B が成り立ちますね。 よって、 AC = 1/r×B×r×B = B² となるわけです。 これを使って、問題を解いてみましょう。 問題 等比数列において連続する3項であるa, b, cが、 abc = 26 abc = 216 となり、等比数列の和の公式を求めることができました。 階差数列を利用して等比数列の和を求める方法 最後の方法は、 等比数列の階差数列を利用する方法 です。 ※前提知識として、「階差数列の定義や利用・活用について」にて紹介している

Sの公式 等比数列 高校数学 数列 ２８ Youtube

A n = A n B a_n=AnB a n = A n B タイプ→等差数列だからすぐに一般項が分かる; 数列の基本5｜階差数列の考え方は簡単！ 階差数列の公式 いわゆる 階差数列の公式は一見複雑な形をしているように見えるためか，階差数列に苦手意識をもっている人は少なくないようです． しかし， 階差数列のイメージは単純なので，実は 階差数列 数列の基本7｜ 等差×等比型の数列の和は引き算がポイント 等差数列 3, 5, 7, 9, 等比数列 2, 6, 18, 54, を考えます． このような 等差×等比型の数列の初項から第 n 項までの和は， n を使って表すことができます．

A n = A n 2 B n C a_n=An^2BnC a n = A n 2 B n C タイプ→階差数列が等差数列になる; 等差数列・等比数列の解き方、階差数列・漸化式をスタサプ講師がわかりやすく解説！ 大学受験において頻出単元の1つである「数列」。 公式や考え方をしっかりと覚えて、確実に得点していきたい単元だ。 等差数列や等比数列の一般項だけでなく、数列の和の計算についても紹介。 さらに、Σ（読み方は「シグマ」）の公式や計算方法、階差数列や漸化式の基本 が等比数列 → は 見出しの通り、 とすれば実際に と出来ます。 等比数列の和は公式化されており、和分差分学的な方法に依るよりも公式を覚えて運用するほうが手早く計算できますが、恒等式 を理解していると見通しの良くなる場面は多くあります。例の

等比数列の和の公式について質問させてください。 先生のページでは、項比rから－1するという形になっていますが、 別の書籍等では、1から項比rをマイナスするという形になっているものもあります。 この違いは何に起因するのでしょうか？階差数列は、\({b_n}\) という文字を使って表すことが多いです。 そして、\( 2, 5, 10, 17, 26, 37, \cdots\) のように、 等差、等比でもない数列の一般項を考える場合 この階差数列が役に立つことがあ等差数列の和 にリンクを張る方法 このページの先頭へ ブックマーク 実行履歴 関連ライブラリ 等差数列の和 等比数列の和

等比数列の一般項と和 おいしい数学

高校数学b 階差を利用する和 根号型 対数型 階乗型 受験の月

 \(\{a_n\}\) の階差数列を調べてみると、\(1, 2, 5, 10, 17, \cdots\) となり、等差でも等比でもないようです。 そこで、さらなる階差数列（第二階差数列）を求めてみましょう。 規則性のある数列が見えるまで、階差を何回かとるのもテクニックの \(1\) つです。等比数列の第\(n\)項は、初項に公比を\((n1)\)回だけ掛けた数ってことなので $$\begin{eqnarray}a_n=ar^{n1} \end{eqnarray}$$ こういった公式ができあがるわけですね！ 等比数列の一般項に関する問題解説！ では、一般項の公式を使って問題を解いてみましょう。 階差数列も「数列」なので 階差数列が等差数列なら等差数列として扱いますし、 階差数列が等比数列なら等比数列として扱います。 階差数列の和を求める必要がある場合は それぞれ「等差」か「等比」かによって 扱う公式は異なりますね。

5講 等比数列の和 1節 等差数列と等比数列 問題集 3章 数列

等差 等比数列の和 数学 B 数列 Youtube

・等差数列×等比数列の和は求まる。 ∑ k = 1 n k p r k \displaystyle\sum_{k=1}^nk^pr^k k = 1 ∑ n k p r k というタイプの和です。 p = 0 p=0 p = 0 が等比数列の和， p = 1 p=1 p = 1 が等差×等比の和， p = 2 p=2 p = 2 までは出題されることがあります。等差数列と等比数列の積の和 「 等差数列をa n, 等比数列をb n とするとき, ∑ k=1 n a n ⋅b n を求めよ 等差数列と等比数列の積の和ですが, 教科書ではあまりにも見事に計算されているので多くの人達は暗 記してないと解けないでしょう数列がわからない人へ 高校数学B「数列」がわからない人は、以下の順でTry ITの映像授業を観て勉強してみてください。 「等差数列と等比数列」に関する13のポイントを覚える 「Σ（シグマ）」に関する5のポイントを覚える 「階差数列」に関する3の

高校数学b 等比数列の一般項 A N Ar N 1 受験の月

覚えなくていい 等比数列の和 東大生の高校数学ブログ

4 等差数列の和 前の章で，等差数列の一般項について学習しました。ここでは，その和について考えてみることにしましょう。 ここで，初項 3，公差 2，項数 10 の等差数列 3，5，7，9，11，13，15，17，19，21 を考え，その和を求めてみましょう。はい、 (1)は簡単です。 a n =n (2n1) です。 次に (2)の第n項目は、 a n =122 2 2 3 2 4 2 5 2 n1 より、初項1、公比2、項数nの等比数列の和ですから、 となります。 ＜先 生＞ さらにこの数列 {a n }の初項から第n項までの和も、∑の公式を使えば簡単に求められるんだったね。 さて、それでは、今日の問題を考えてみようか。の4つをご紹介いたします。 等比数列の階差数列は、(r – 1)倍の等比数列になる まずは、

数列の和と階差数列 Taustation

高校生 等比数列のノート一覧 Clear

幾何数列）は、隣り合う二項の比が項番号によらず等しい数列を言う。各項に共通する その一定の比のことを公比（こうひ、英 common ratio）という。 例えば 4, 12, 36, 108, という数列 ∞ n=1 は、各項が直前の項に 3 を掛けたものになっているから、初項が 4, 公比が 3 の等比数列である。 公比 r は r= an1階差数列とは の階差数列といいます。 つまり、隣同士の差をとったときにあらわれる数列のことです。 （ ）内は第1項から第（n1)項までの和である。これをΣ記号を使って表すと Σの計算の仕方この数列は、左の数字に2をかけると次の数字になるという規則に従っている。 このような数列の最初の項のことを、 初項 という。 一定の数を 足す ことで次の項が得られる数列 のことを 等差数列 と言い、 一定の数を かける ことで次の項が得られる数列 のことを 等比数列 という。 等差数列において足す数字のことを 公差 （dで表す）と言い、等比数列におい

等差 等比型

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

 等比数列の和の応用編 ～分数でやってみよう！～ 次は、分数でやってみましょう。 1/2 ＋ 1/4 ＋ 1/8 ＋ 1/16 ＋ 1/32＝？ これは 左の数「×1/2」⇒ 右の数 の等比数列です。 ★ ⇒ 1/2 ＋ 1/4 ＋ 1/8 ＋ 1/16 ＋ 1/32 ★× 1/2 ⇒ 1/4 ＋ 1/8 ＋ 1/16 ＋ 1/32 ＋1/64 等比数列の一般項がわかったところで、等比数列のよく使う性質を紹介しておきます。 それは簡単に書くと次のようになります。 等比数列の連続する3つの数 a 、 b 、 c がこの順で並んでいるとき、これらには次の関係がある。 a × c = b 2 例えば先ほど等比数列の和の公式① このような等比数列があったとしましょう。 この数列は「初項5、公比3、項数6の等比数列」です。 公比が3で1より大きいのでこの公式を使います。 \begin {eqnarray} \displaystyle S_ {6}&=&\frac {a (r^ {n}1)} {r1}\\ &=&\frac {5 (3^ {6}1)} {31}\\ &=&\frac {5 (7291)} {2} &=&10 \end {eqnarray} したがって、等比数列の和を求めることができました。

高校数学 数b ６８ 等比数列とその和 Youtube

写真の水色の線のところなんですけど見えにくかったらすみません 下の２行です Clear

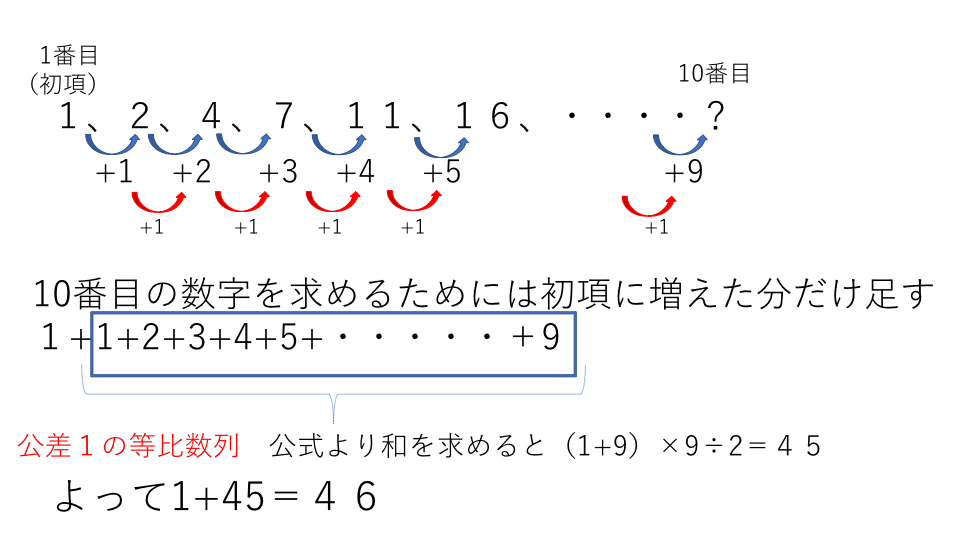
数学B ： 数列 公式集 数式の表示がおかしいときは こちら をご覧ください。 印刷用PDFは こちら 絶対憶える 憶える 復習A n = A n 3 B n 2 C n D a_n=An^3Bn^2CnD a n = A n 3 B n 2 C n D タイプ→階差数列の階差数列が等差数列 解説 問題の数列 (Aとします)の差を並べると、,18,16,14,12 となります (階差数列=B)。 Bの差は全て2で「減る」タイプの等差数列 になっています。 減るタイプは公式が少し変わって「N番目の数=はじめ ー {差× (N1)}」になることに気を付けましょう。 Aの10番

高校数学b 等比数列の和の公式の証明 受験の月

高校数学b S と等差 等比数列の和 映像授業のtry It トライイット

等比数列（とうひすうれつ、英 geometric progression, geometric sequence; 中学受験の算数で出題される単元 「等差数列」「等比数列」「階差数列」 。 この単元では、規則性の把握が求められます。 算数は論理的に物事を考える能力を身に付けるための学問ですが、等差数列・等比数列・階差数列の問題は、まさしくこの 論理的思考 が求められる問題であると言えます。 もともと、これらの数列に関する問題は小学校では教育範囲に入っ数学において、算術数列と幾何数列の項ごとの積によって与えられる、算術–幾何数列 (arithmetico–geometric sequence) は、象徴的に「算術⋅幾何数列」とか「(等差)×(等比)型の数列」などのようにも呼ばれる。

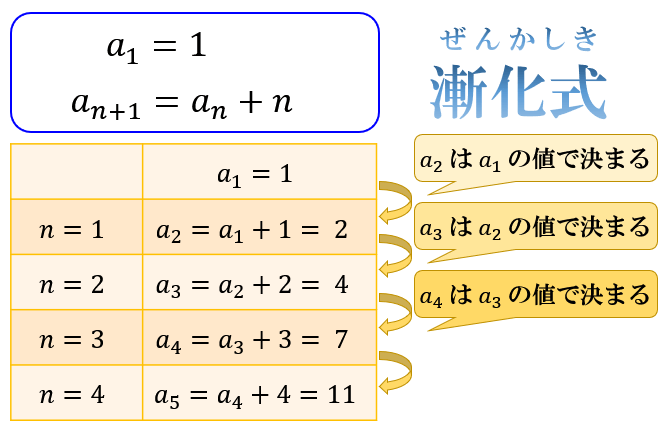
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

階差数列・和と一般項の関係 階差数列 階差数列をbn とするとき an = a1 n∑ 1 k=1 bk (n = 2) 和と一般項の関係 an = Sn −Sn 1 (n = 2) a1 = S1 基本漸化式4 パターン an1 = an p (p は定数) 等差数列 ※p は公差 an1 = ran (r は定数) 等比数列 ※r は公比等差数列の和 等比数列の和 特殊数列の和 無限等比級数の和等比数列，循環数列 群数列 自然数の累乗の和 → 携帯版は別頁 数列の「各項の差」からなる数列を元の数列の階差数列と言います。 例 元の数列よりもその差から作った階差数列の方が簡単な規則性を持っていることが多いので，階差数列で規則性を見つけて，元の数列の一般項を求めることができます。 階差数列の定義 元の数列を { a n }，階差数列を { b n }で

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

Sの公式 等比数列 高校数学 数列 ２８ Youtube

等比数列（和） 1044 6．等比数列の和の公式の使用例 748 7．ジグザグ型の数列 537 8．調和数列 215 9．シグマの意味 1245 10．シグマの公式 849 11．階差数列（一般項） 1117 12．階差数列（和） 553 13．和から一般項を求める 848 14．「等差数列」×

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

特殊な和の求め方その２ 等差 等比編 高校数学の知識庫

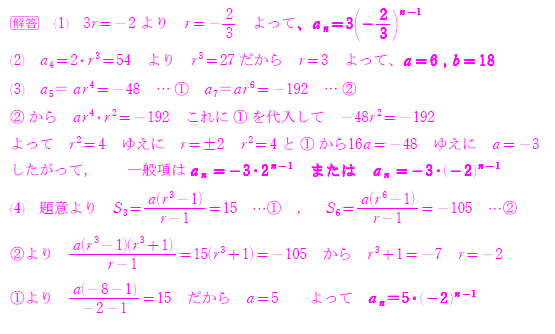
学年末b 数列 追試対策 等比数列 階差数列 数 Bを ぶっ飛ばせ

高校数学b 階差数列から一般項を求める １ 練習編 映像授業のtry It トライイット

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

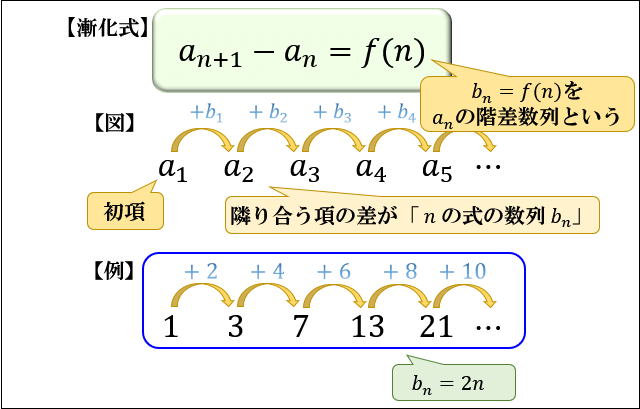
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

高校数学の等比数列の和の公式を分かりやすく 大学受験対策にも タロウ岩井の数学と英語 Note

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

等差 等比型

高2数学b等比数列階差数列の和画像の の部分を教えてください Yahoo 知恵袋

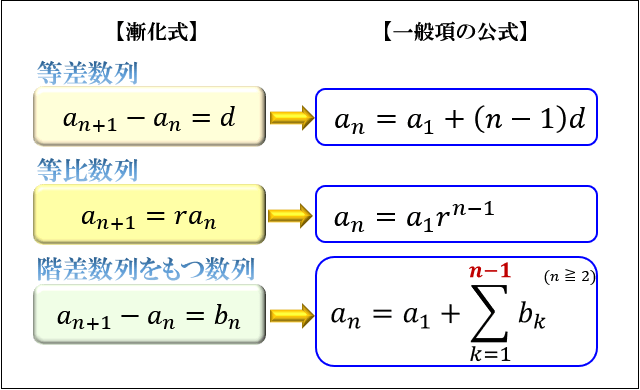
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

高校数学b 等差数列と等比数列の共通項の数列の一般項 受験の月

等比数列の一般項と和 おいしい数学

等比数列の和について 数学 苦手解決q A 進研ゼミ高校講座

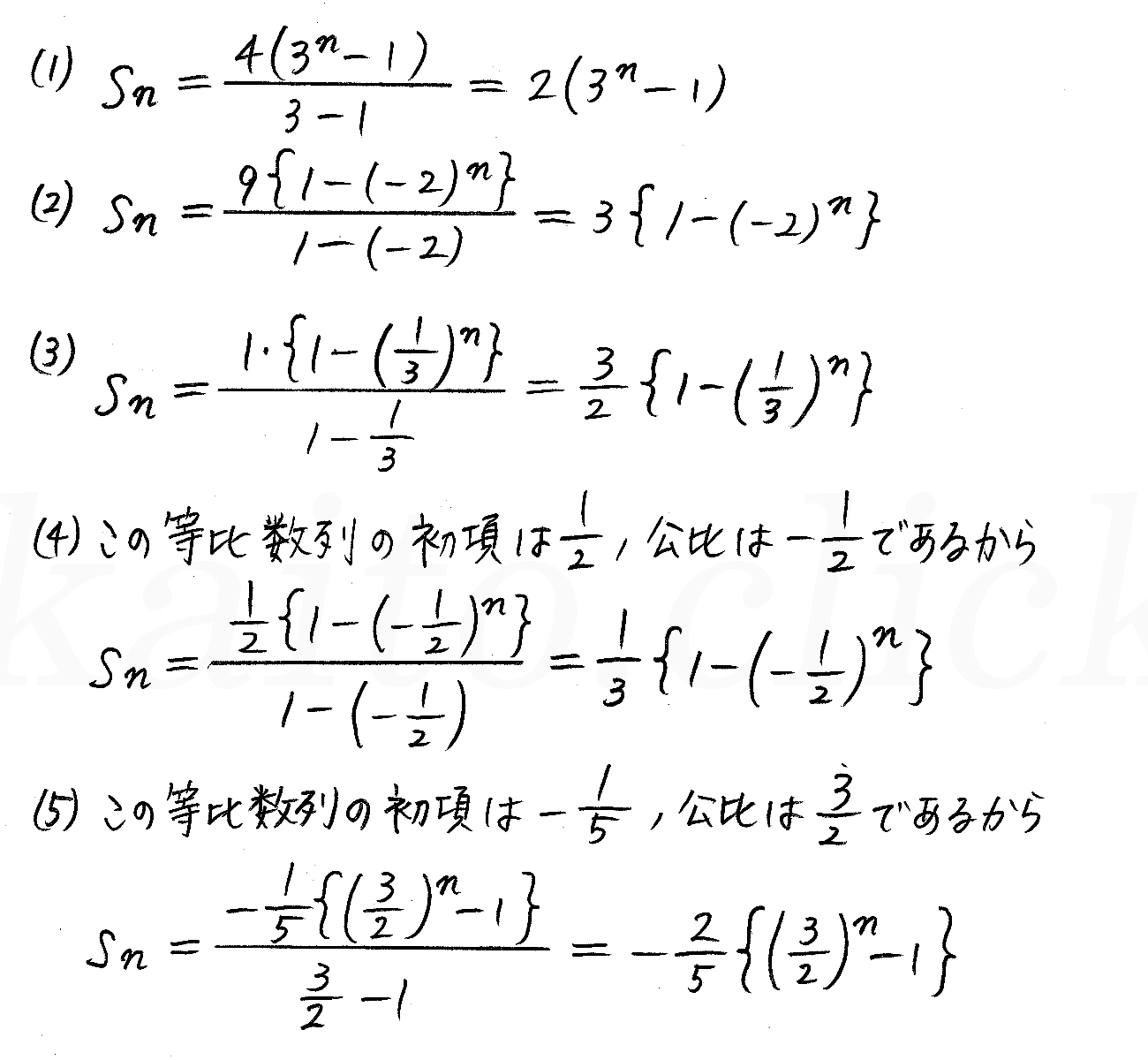
改訂版 クリアー数学b P153 17 等比数列の和

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

改訂版 クリアー数学b P154 17 等比数列の和

3

等差数列の和の公式と階差数列の公式はおなじでしょうか 問 Yahoo 知恵袋

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

2 5 14 41 122 365の一般項を求めよ が分かりません Clear

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

等差 等比 の和 2次式 等比 の和 おいしい数学

1乗和 2乗和 3乗和の公式 導出法から理解しよう

高校数学b S と等差 等比数列の和 映像授業のtry It トライイット

例題で学ぶ高校数学 階差数列

2

階差数列の一般項anを求める問題の途中式を詳しく教えて下さい 式の作り Yahoo 知恵袋

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

高校数学の等比数列の和の公式を分かりやすく 大学受験対策にも タロウ岩井の数学と英語 Note

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

数列の基本５ 階差数列の考え方は簡単 階差数列の公式

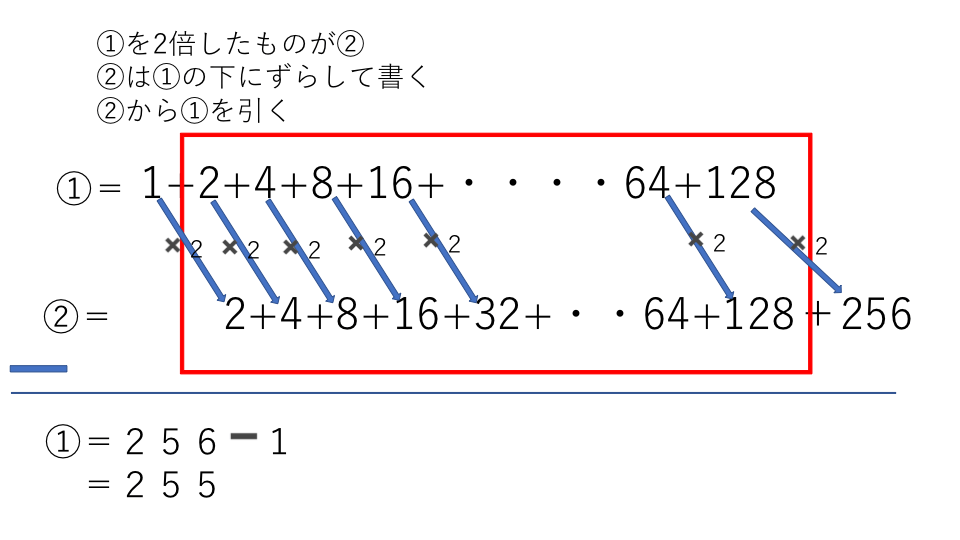
中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

高校数学b 等比数列 A N の一般項 ２ 練習編 映像授業のtry It トライイット

高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月

等差数列をグラフにしてみよう 父ちゃんが教えたるっ

2

数列と級数 京極一樹の数学塾

等差数列の和の最大 数学b 等差数列と等比数列 5 Youtube

階差数列

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

なんで初項2 公比2の等比数列とわかるのですか Clear

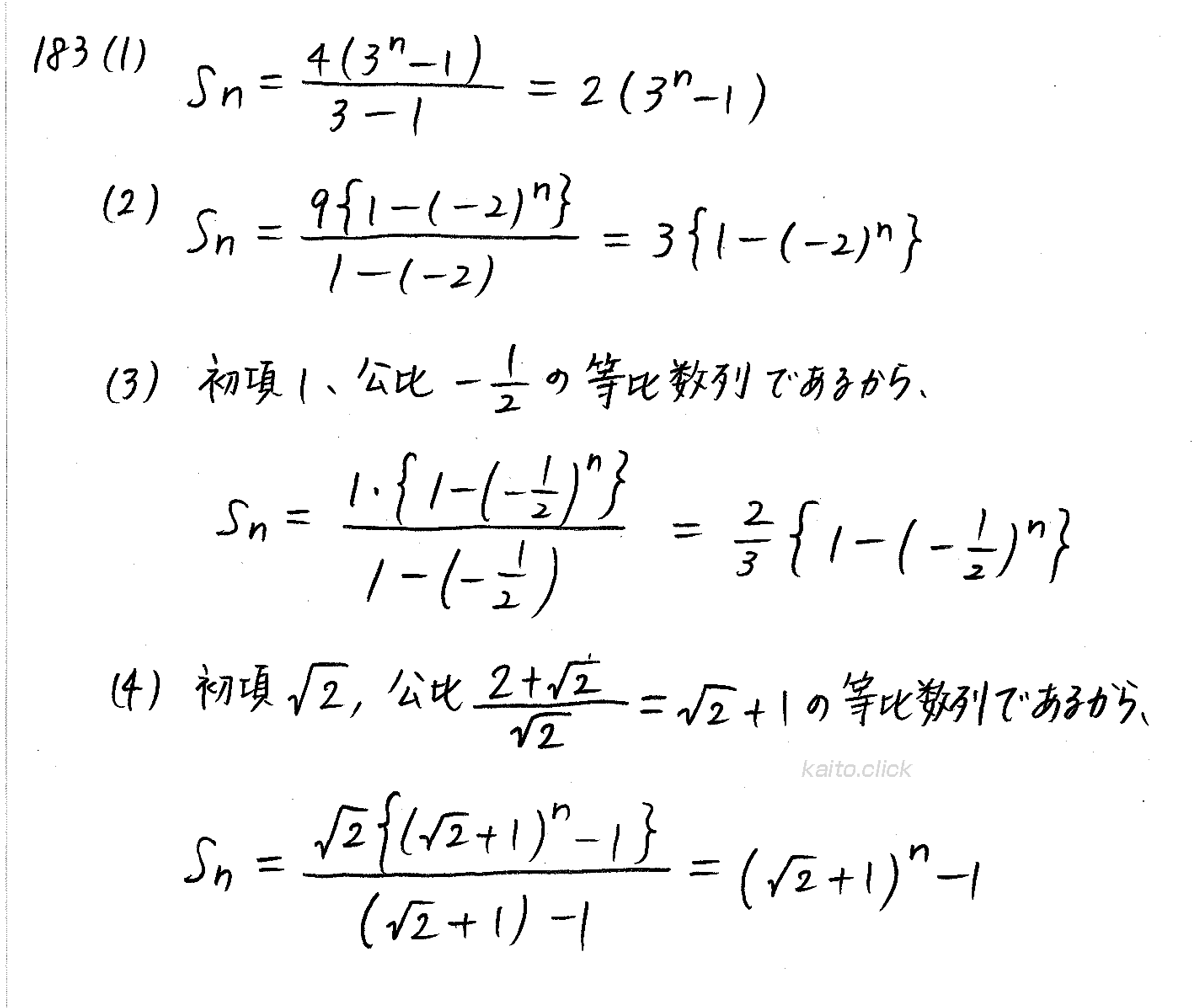
クリアー数学b 数b P141 17 等比数列の和

変形階差形 F N タイプ ４ 怜悧玲瓏 高校数学を天空から俯瞰する

数列とは コトバンク

漸化式で表される数列とその一般項 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信

数列の基本２ 等差数列の和の公式 と 等比数列の和の公式

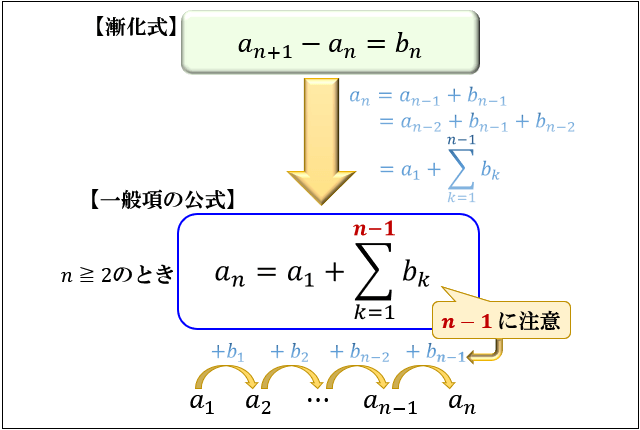
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

詳説 数学ｂ 等差数列 等比数列 高校生 数学のノート Clear

1

2

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

3

中学受験 差 階差数列 を利用する問題の解き方 無料プリントあり そうちゃ式 受験算数 新1号館

階差数列

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

数学用語解説 数b 数列

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

数学b 数列 等差数列 等比数列 型 オンライン無料塾 ターンナップ

いろいろな数列の和 N 2のとき と定義する問題としない問題があります 数学 教えて Goo

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

階差数列

高校数学b 等差数列の和s Nの最大 最小 受験の月

いろいろな数列の和 N 2のとき と定義する問題としない問題があります 数学 教えて Goo

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

数学b 数列 和から一般項を求める オンライン無料塾 ターンナップ

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

高校数学b 等比数列 A N の和 １ 映像授業のtry It トライイット

階差数列のちょっとした小手技

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

等差数列 等比数列 階差数列 基本３パターン の漸化式 数学の偏差値を上げて合格を目指す

階差型の数列 おいしい数学

3講 等差数列の和 1節 等差数列と等比数列 問題集 3章 数列

2

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

1

誤答から学ぼうシリーズ 等差数列 等比数列 型の数列の和 ほのぼの数学頑張ろう